センター2019物理第２問B 「導体棒にはたらく力とキルヒホッフの法則」

2019.08.15
スポンサーリンク

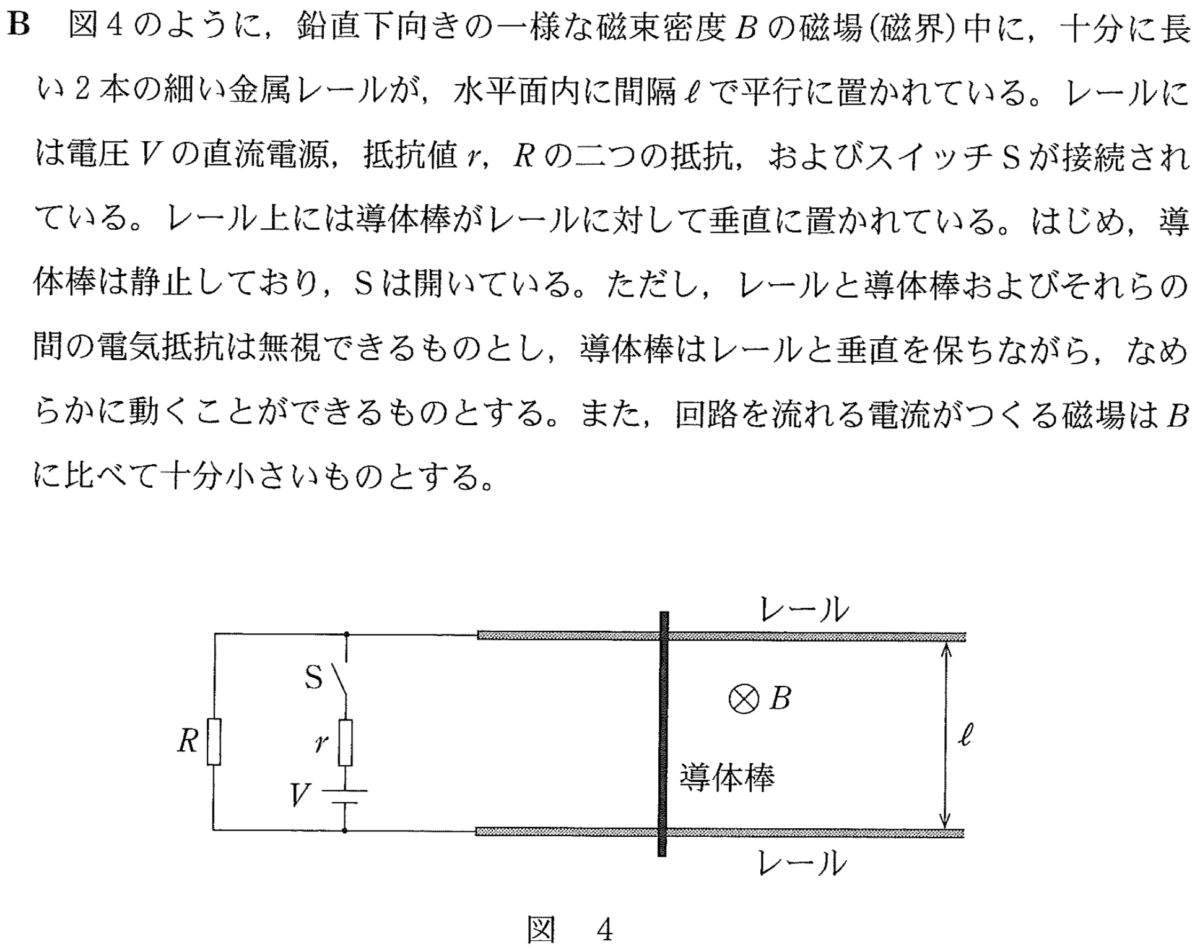
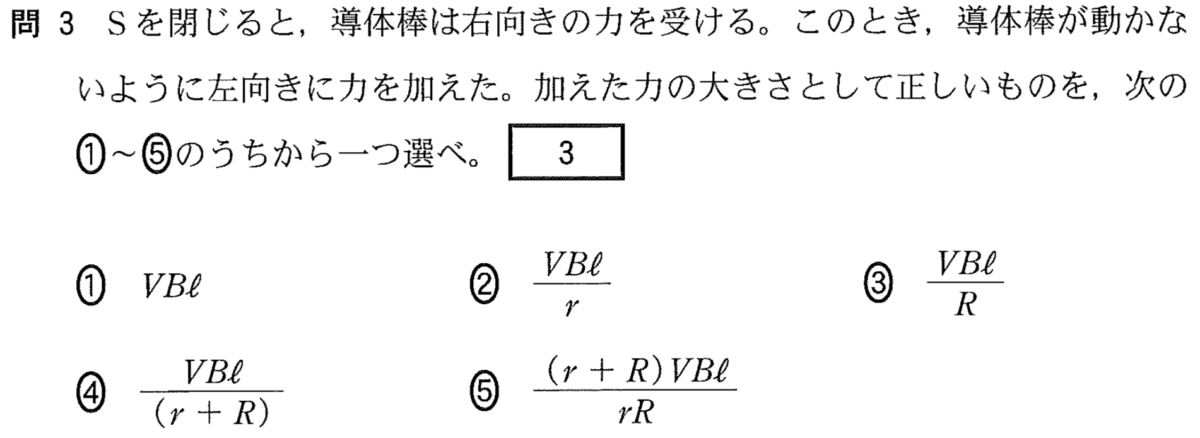
導体棒が動かない→力のつり合い

物理が苦手な文子
レールの上を導体棒が動くこのタイプの問題は見たことがあるわ。
物理が得意な秀樹
まぁよくあるタイプの問題ではあるんだけど，ちょっと難しくなっている点もあるので，しっかりと確認していこう。
物理が苦手な文子
見たことがあるとはいえ，何から始めればいいのか分からないわ。
物理が得意な秀樹
とりあえず，何を求めるのかを確認しておこう。
物理が苦手な文子
「左向きに加えた力の大きさ」ね。
物理が得意な秀樹
そうだね。じゃあその力の大きさを求めるために必要な情報はないかな。
物理が苦手な文子
何だろう？「導体棒は右向きの力を受ける」とも書いてあるわね。右向きの力と左向きの力があるっていうこと？
物理が得意な秀樹
そうだね，問題文に書いてあるからね。その２つの力の関係は？
物理が苦手な文子
２つの力の関係？えっと，そうか，問題文に「導体棒が動かないように左向きの力を加えた」とあるから，「動かない」ということは２つの力がつり合っているっていうことかな？
物理が得意な秀樹
そう，２つの力はつり合っているんだ。問題では左向きの力の大きさを答えることになっているけど，右向きに働いている力の大きさが分かればいいよね。
物理が苦手な文子
なるほど。問題文には「Sを閉じると導体棒は右向きの力を受ける」とあるわね。まずはSを閉じると電流が流れるわよね。
物理が得意な秀樹
電流が流れるね。
物理が苦手な文子
で，磁場があるから，その電流が磁場から力を受けるということね。
物理が得意な秀樹
そうだね。その力の向きと大きさは分かる？
物理が苦手な文子
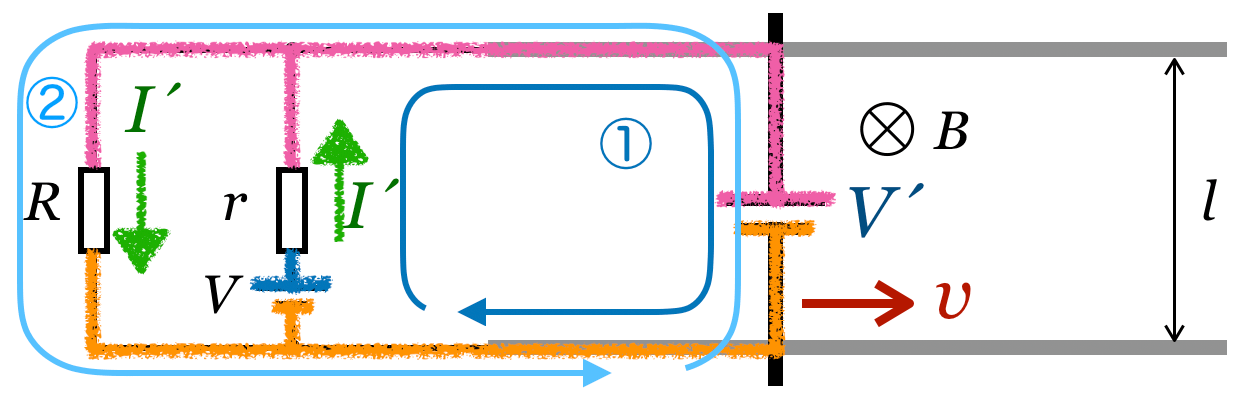
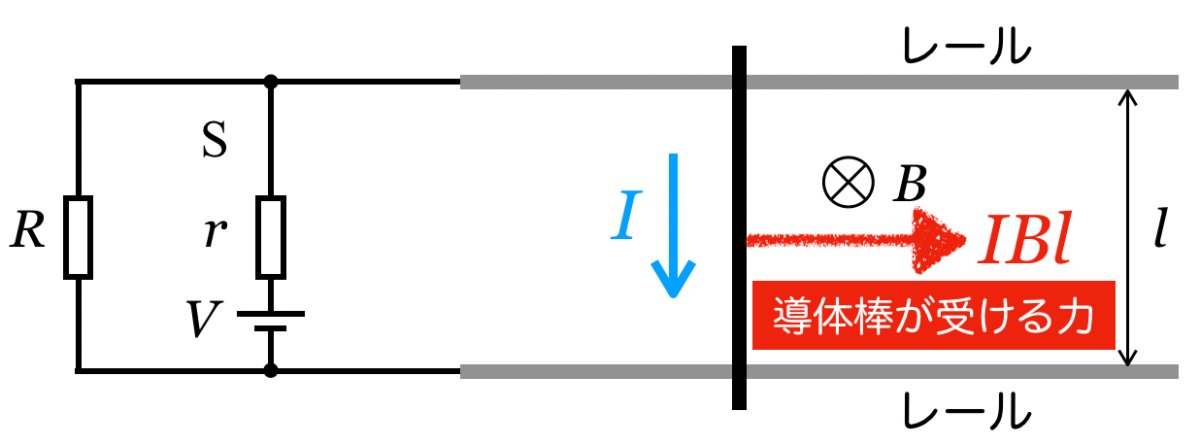
力の向きはフレミング左手の法則で求めるのね。導体棒には図の上から下に電流が流れて，磁場は紙面に対して表から裏の向きだから，フレミング左手の法則で考えると，力の向きは右向きね。
物理が得意な秀樹
その通りだ。問題文にも導体棒にはたらく力は右向きとあったね。その力の大きさは？
物理が苦手な文子
えっと，確か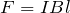F=IBlだったかな。
物理が得意な秀樹
そう，導体棒を流れる電流を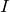Iとすると，こうだね。
物理が苦手な文子
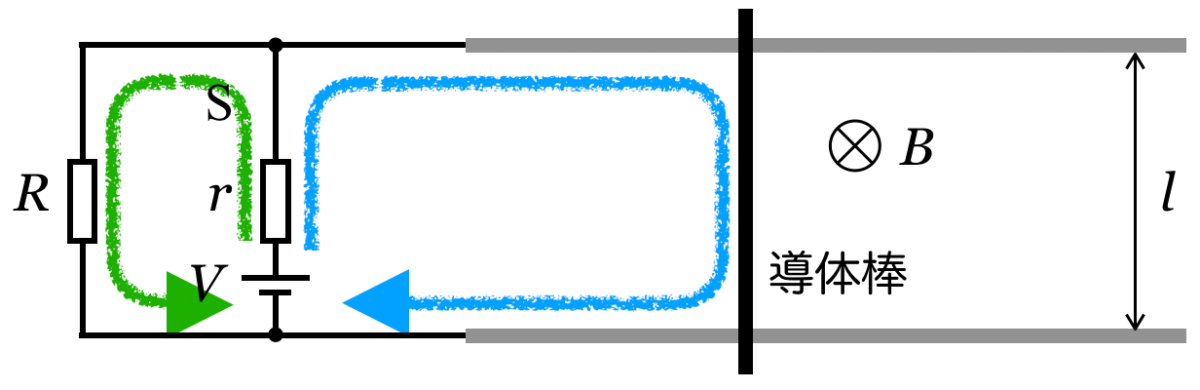
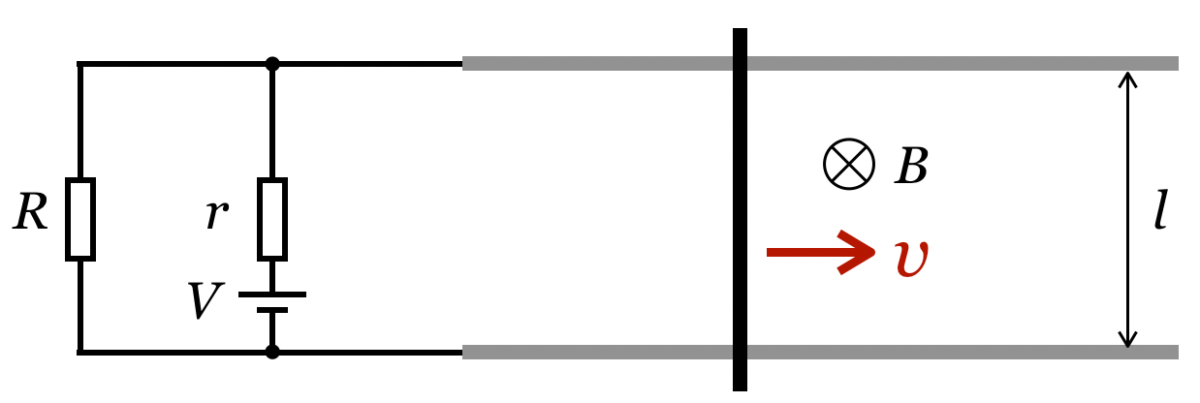
力の矢印を描いてみるとこんな感じね。
物理が得意な秀樹
その右向きの力に対して，導体棒が静止するように左向きの力を加えたということだね。

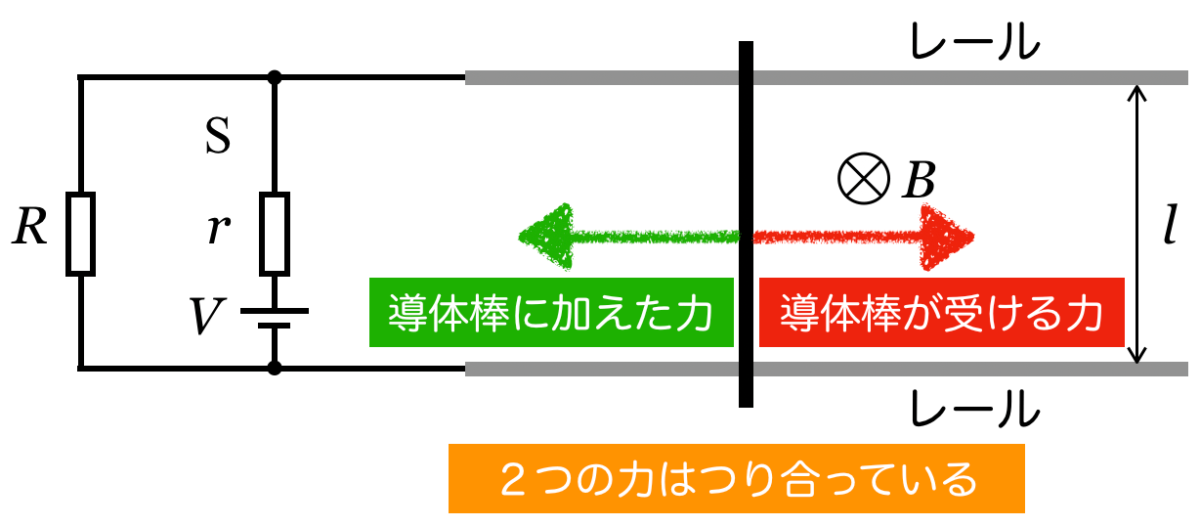
抵抗Rには電流が流れない

物理が苦手な文子
ということは，答えは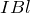IBlとしたいところだけど，選択肢がないわ。
物理が得意な秀樹
そうなんだよ。電流の強さ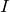Iを求めなきゃダメなんだ。
物理が苦手な文子
あっそうか，導体棒を流れる電流を求めなきゃダメなのね。じゃあまず，電池は１つしかないから，この電池から右の導体棒側と，左の抵抗側に電流が別れるわよね。
物理が得意な秀樹
普通はそうだよね。
物理が苦手な文子
「普通は」っていうことは，この場合は違うっていうこと？
物理が得意な秀樹
そう，違うんだ。この問題ではレールや導体棒の電気抵抗は無視できるので，電流は電気抵抗のない導体棒側にだけ流れんだよ。
物理が苦手な文子
電気抵抗が0だと，そっちにだけ電流が流れるのね。
物理が得意な秀樹
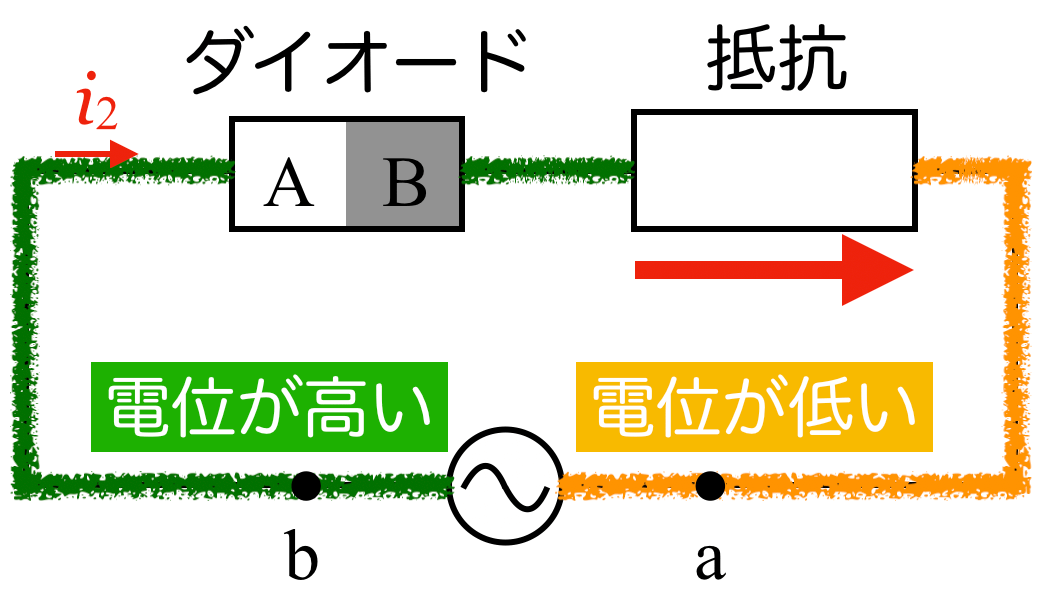
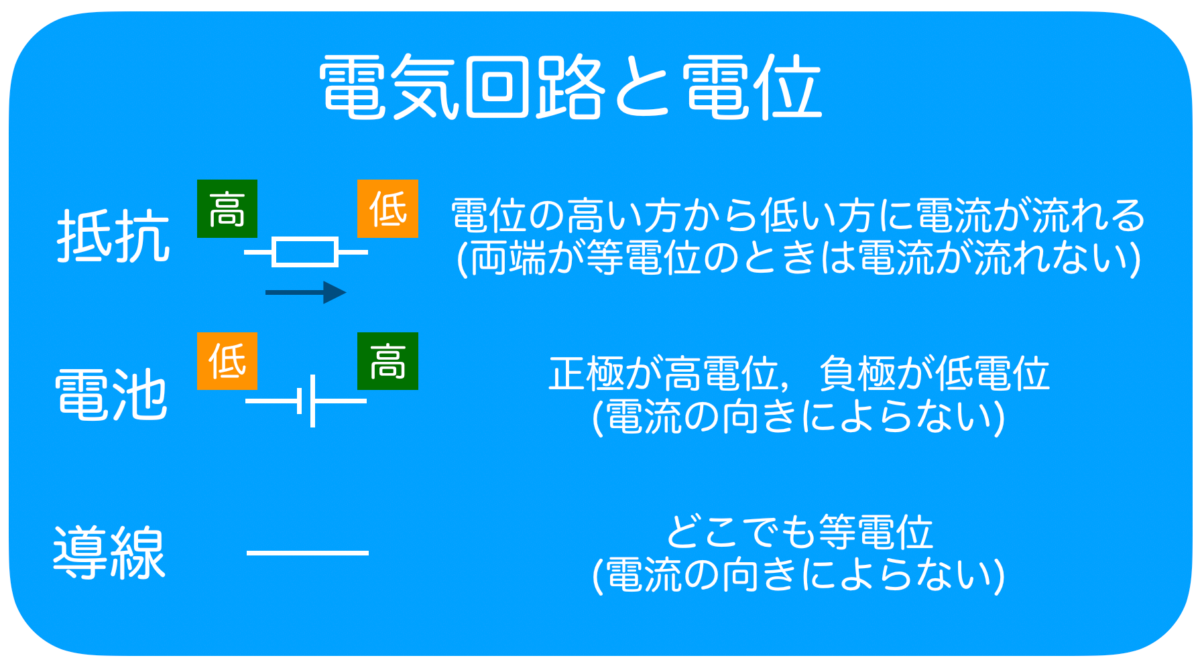
そのことは覚えておいた方がいいんだけど，一応電位の考え方で説明するね。電気回路の電位はこんな風に考えるんだ。
物理が苦手な文子
まぁ，なんとなく分かるわ。この電位の考え方をどう使うの？
物理が得意な秀樹
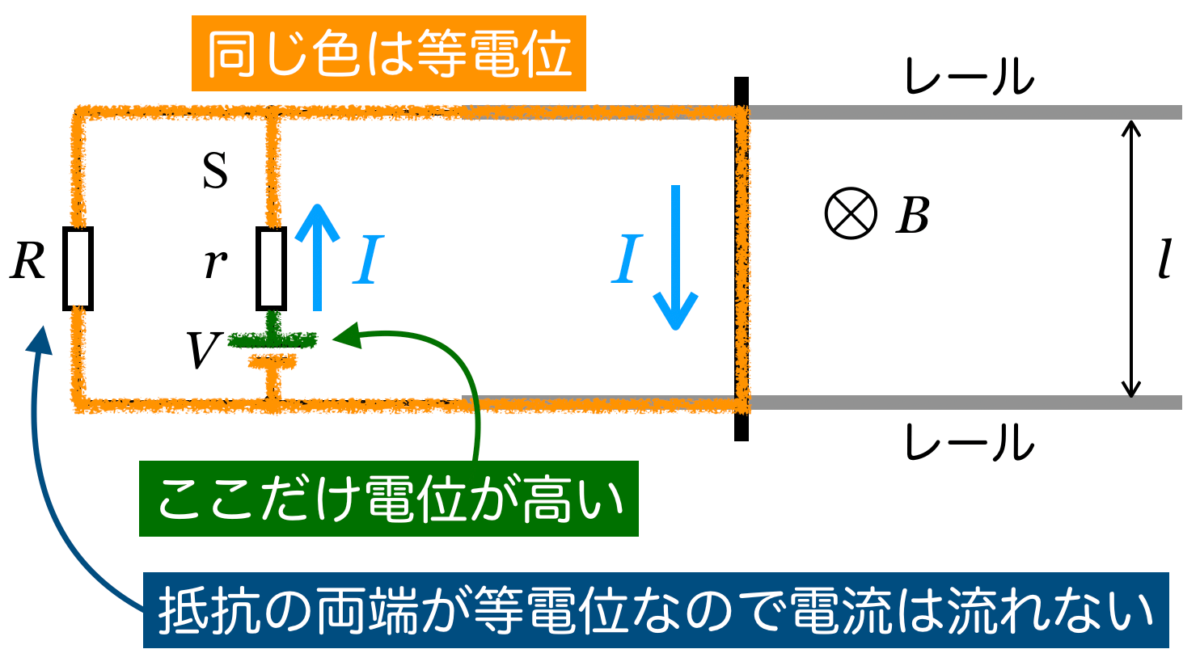
このルールに従って，東電位のところに色を塗ってみるよ。
物理が苦手な文子
導体棒の電気抵抗は0だから，導線と同じと考えていいのね。左側の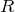Rの抵抗の両端の電位が等しくなっているので，この抵抗には電流が流れないっていうことね。
物理が得意な秀樹
そうなんだよ。だから導体棒側にしか電流が流れないんだね。
物理が苦手な文子
あとはこの電流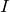Iを求めればいいのね。これはオームの法則でいいわよね。

    $$I=\frac{V}{r}$$

物理が得意な秀樹
それでいいね。ようやく答えを出せるね。
物理が苦手な文子
求める力の大きさ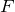Fは，

    \begin{eqnarray*}F&=&IBl\\&=&\frac{VBl}{r}\end{eqnarray*}

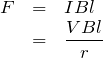
物理が得意な秀樹
そうだね。答えは②だ。

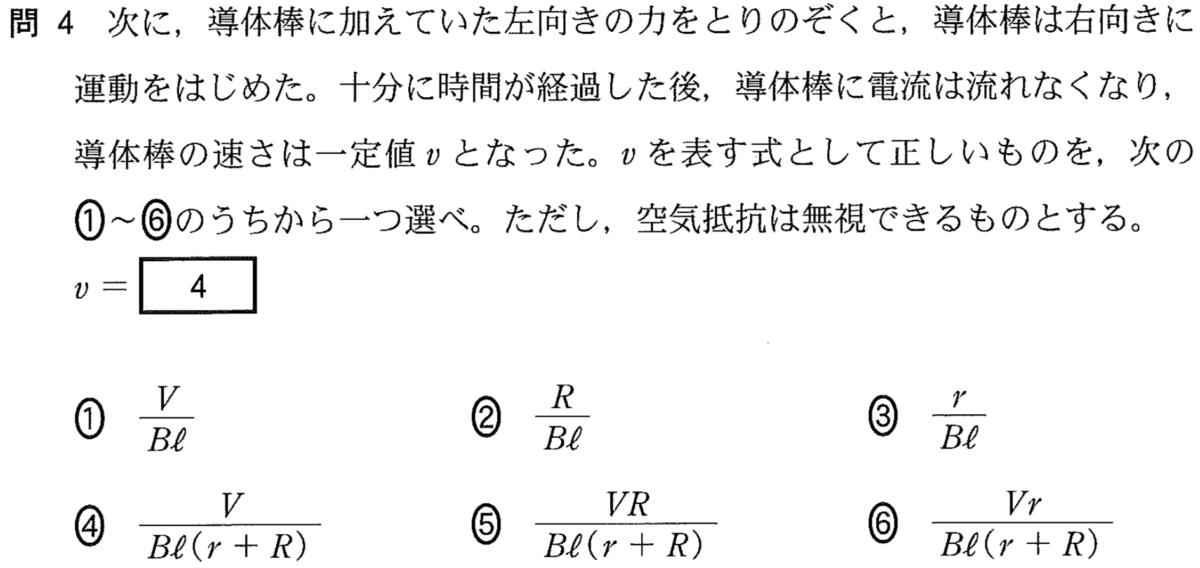
誘導起電力が生じて電流が流れない

物理が苦手な文子
今度は加えていた左向きの力をとりのぞいたのね。そうすれば当然右向きの力ははたらいているんだから，右に動き出すわよね。
物理が得意な秀樹
そういうことだね。
物理が苦手な文子
でも，十分に時間が経過したら，導体棒に電流が流れなくなったっていうのは，どういうことなの？電池はつながったままなのよね。
物理が得意な秀樹
電池はつながったままだね。電流が流れなくなったのは，導体棒に誘導起電力が生じたからなんだ。
物理が苦手な文子
誘導起電力？なんか聞いたことはあるけ・・・
物理が得意な秀樹
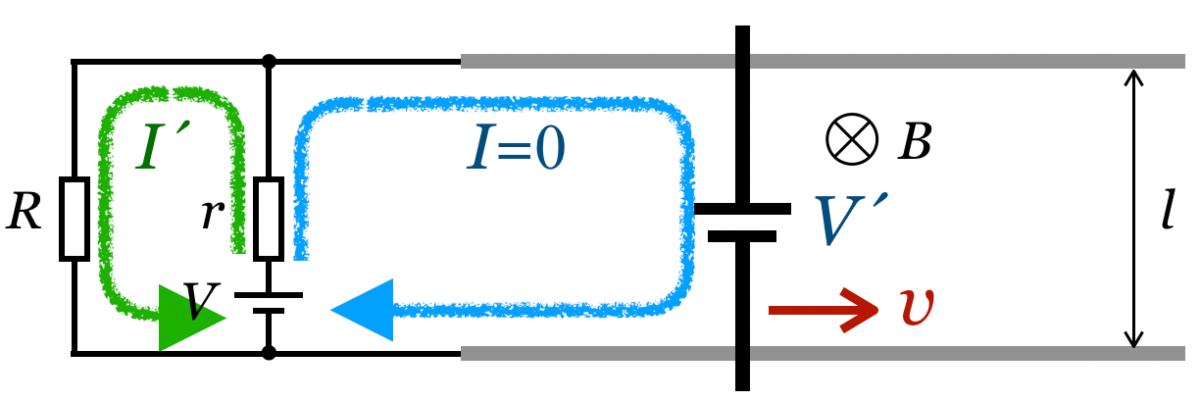
簡単に言うと，導体棒が電池になったんだね。この誘導起電力の向き（電池の向き）の求め方にはいろいろな方法があるんだけど，この問題では「電流が流れなくなった」とあるので，電流が流れなくなるような向きに誘導起電力が生じると考えていいね。こんな感じだ。
物理が苦手な文子
導体棒が電池になるのはいいけど，電池になったのに電流が流れないの？
物理が得意な秀樹
電池になったから電流が流れないんだよ。
物理が苦手な文子
まぁそういうことか。
物理が得意な秀樹
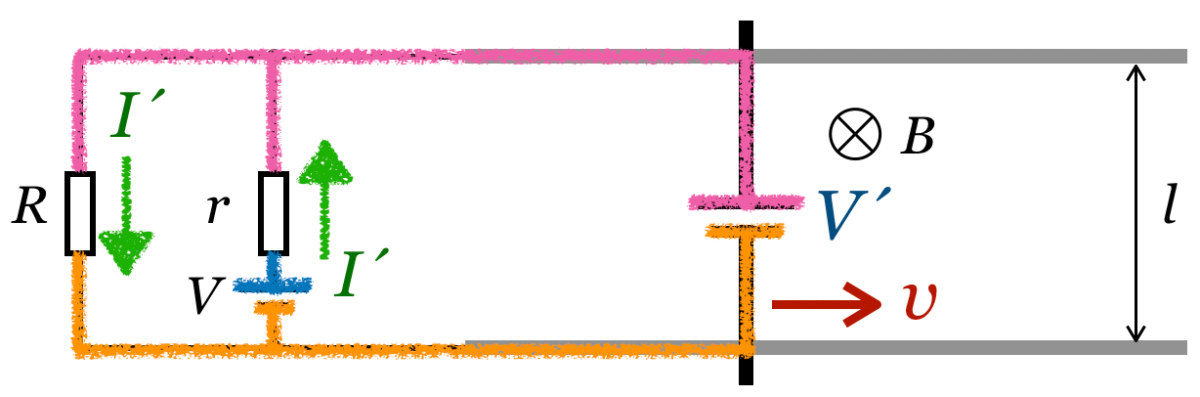
それじゃあ電位についても考えてみようか。回路の電位については，さっきの考え方と一緒なので，同じ電位のところには同じ色を塗ってみるよ。
物理が苦手な文子
さっきのこのルールに従っているのね。

キルヒホッフの第２法則

物理が得意な秀樹
あとはキルヒホッフの第２法則の式を立てるだけだ。
物理が苦手な文子
キルヒホッフの第２法則は，この場合でも使えるの？
物理が得意な秀樹
キルヒホッフの第２法則は，電気回路の電位に関する関係式なので，回路になっていれば使えるよ。特に電池が複数ある場合に使うことが多いけどね。
物理が苦手な文子
この問題でも電池が２つあるということね。
物理が得意な秀樹
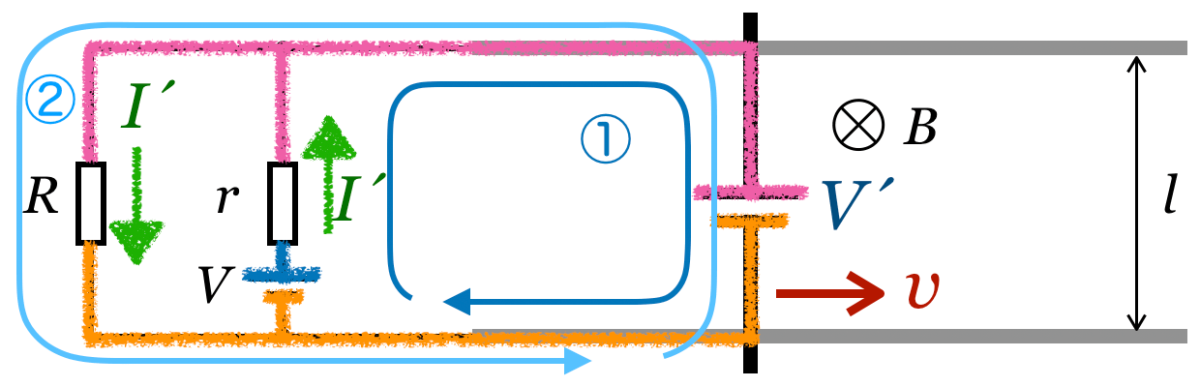
そういうことだね。じゃあ，右側の回路①と外回りの回路②で式を立ててみようか。
物理が苦手な文子
えっ，導体棒には電流が流れていないけど，式を立てていいの？
物理が得意な秀樹
キルヒホッフの第２法則の式は，電位の関係式だから，電流が流れていてもいなくても関係がないんだ。「電気回路と電位」のルールに従って，電位の関係式を立ててみよう。
物理が苦手な文子
なるほど，こういうこと？
①は，

    $$V-rI'-V'=0$$

②は，

    $$V'-RI'=0$$

物理が得意な秀樹
いいね。で，何を求めるんだっけ？
物理が苦手な文子
あれっ？求めるのは導体棒の速さね。この２つの式には出てこないわね。
物理が得意な秀樹
この式では導体棒に生じる誘導起電力を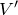V'としたけど，これが導体棒の速さvであらわせるんだ。
物理が苦手な文子
磁場中を運動する導体棒に生じる起電力の式ね。
物理が得意な秀樹
その式だ。キルヒホッフの第２法則から導かれた２本の式と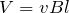，V=vBlからvを求めてみよう。
物理が苦手な文子
計算してみるわ。
②から

    $$I'=\frac{V'}{R}$$

①に代入して

    $$V-r\times \frac{V'}{R}-V'=0$$$$V=\frac{r+R}{R}V'$$


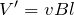V'=vBlなので，

    $$V=\frac{r+R}{R}\times vBl $$$$v=\frac{VR}{Bl(r+R)}$$

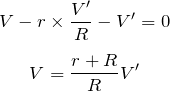
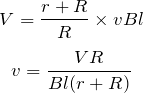
物理が得意な秀樹
計算も合ってるね。答えは⑤だ。
タイトルとURLをコピーしました