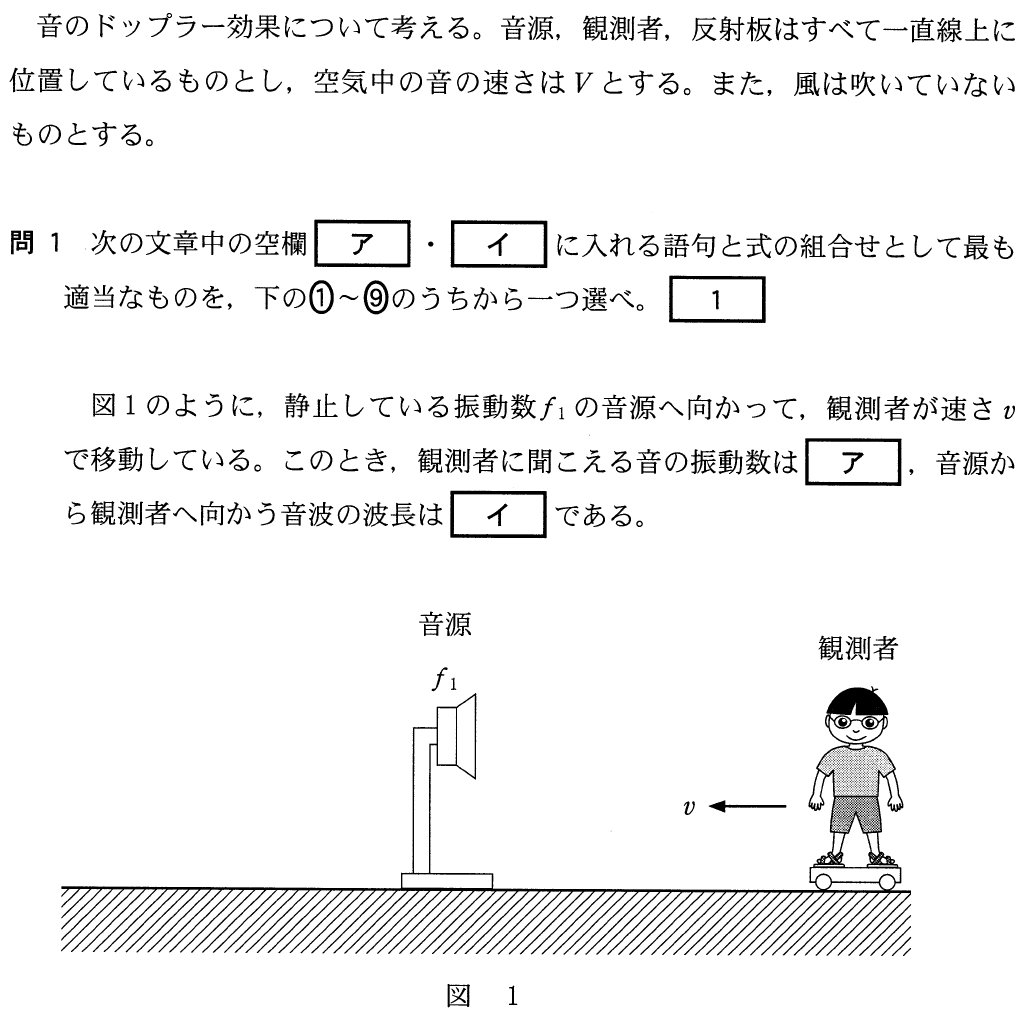

■近づくときの振動数は?
問題としては音源が動いていることのほうが多いけど,この問題のように観測者が動いている場合もあるよね。
最初は観測者が聞く音の振動数ね。ドップラー効果の公式が使えるわね。
ちょっと待って!公式を使わなくても,振動数の大小を聞いているだけの問題だから,わかるでしょ。

なるほど。今は音源と観測者が近づいているので,振動数は大きくなるのね。
波長は音源だけで決まるんだ。音源が動いていれば波長は変わるけど,音源が止まっていれば波長は変わらないよ。

そうなのね。波長が変わらないということは,波の速さと振動数と波長の関係を使うのね。

この式は音に限らず,波の分野ではよく出てくるから覚えてるよね。それじゃあ波長を計算してみよう。
計算と言っても入れるだけね。
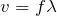
より,
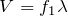
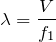
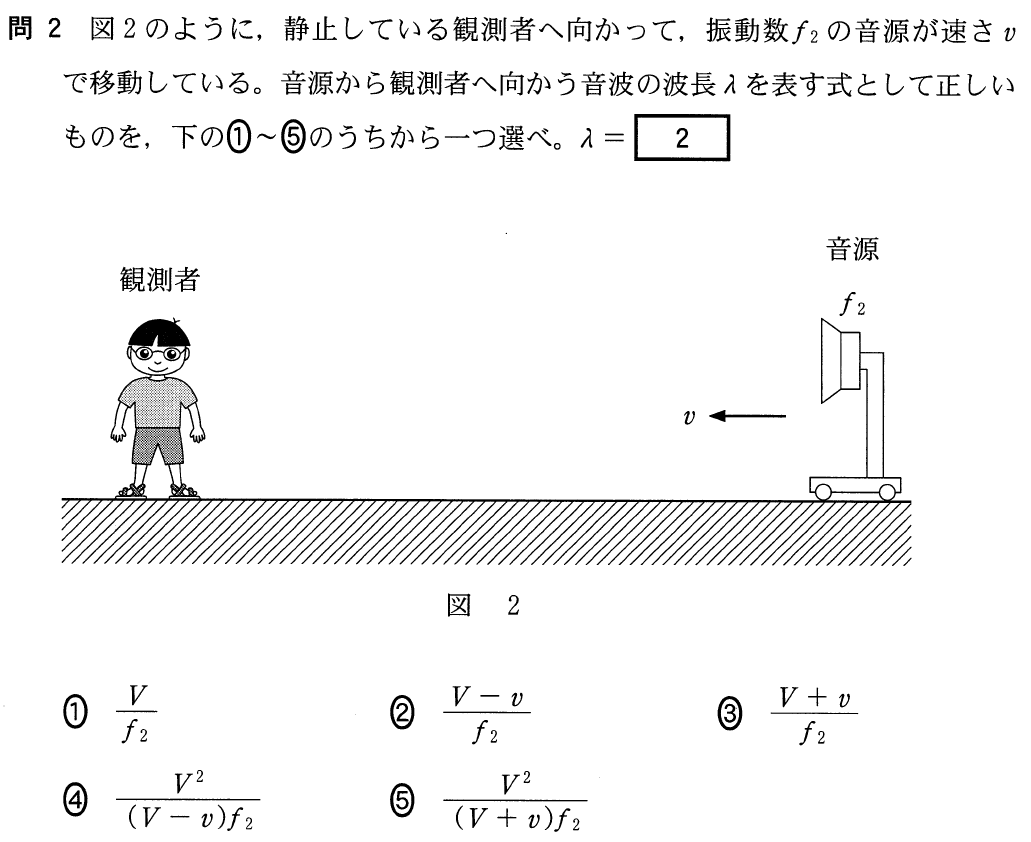
■波長を求める流れを理解しよう
また波長を求める問題だけど,今度は音源が動いているから,波長は変わるのね。
そうだね。波長を求める公式っていうのもあるんだけど,今は公式の出し方も含めて考えてみよう。
パターンが決まってるんだよね。まずは時間を決めるんだ。問題に特に指定がなければ,1秒間を考えるよ。この問題には単位が書かれていないけど,分かりやすく1秒間としちゃうよ。
最初に音源から出た音は1秒後にはどこまで届くかな?
音の速さは

なので,音が届く距離は,速さ
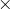
時間=
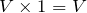
まで届くわ。
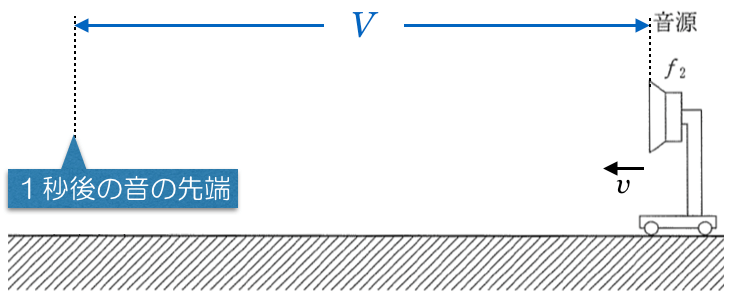
音源の速さは

なので,同様に
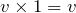
のところにいるわ。
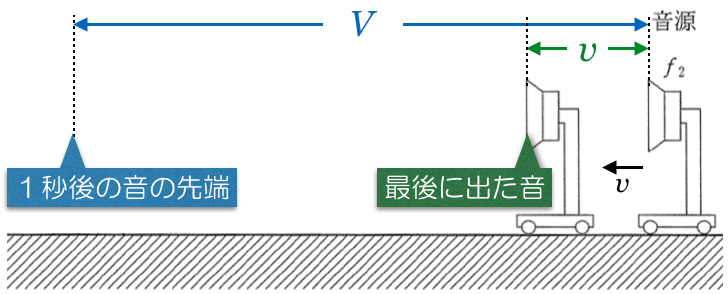
1波長を1つの波だとすると,1秒間に何個の波が出るかな?
振動数って,1秒間に振動する回数よね。振動数が
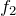
ということは,1秒間に
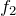
個の波を出しているっていうこと?

そういうことだ。ということは,
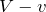
の長さの中に,
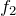
個の波が入っているということになるよね。
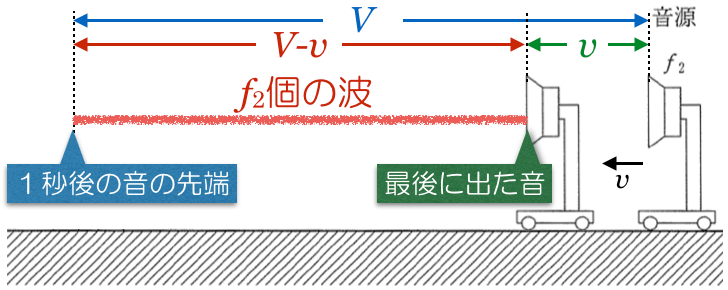
なるほど。つまり,波長
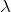
は,
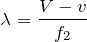
正解だ。答えは②だね。この波長の式を公式として扱っている参考書もあるね。

もちろん,覚えていれば使える場面もあるかもしれないけど,今やったように,この式の導出の流れを分かっていたほうがいいと思うよ。次は問3だ。
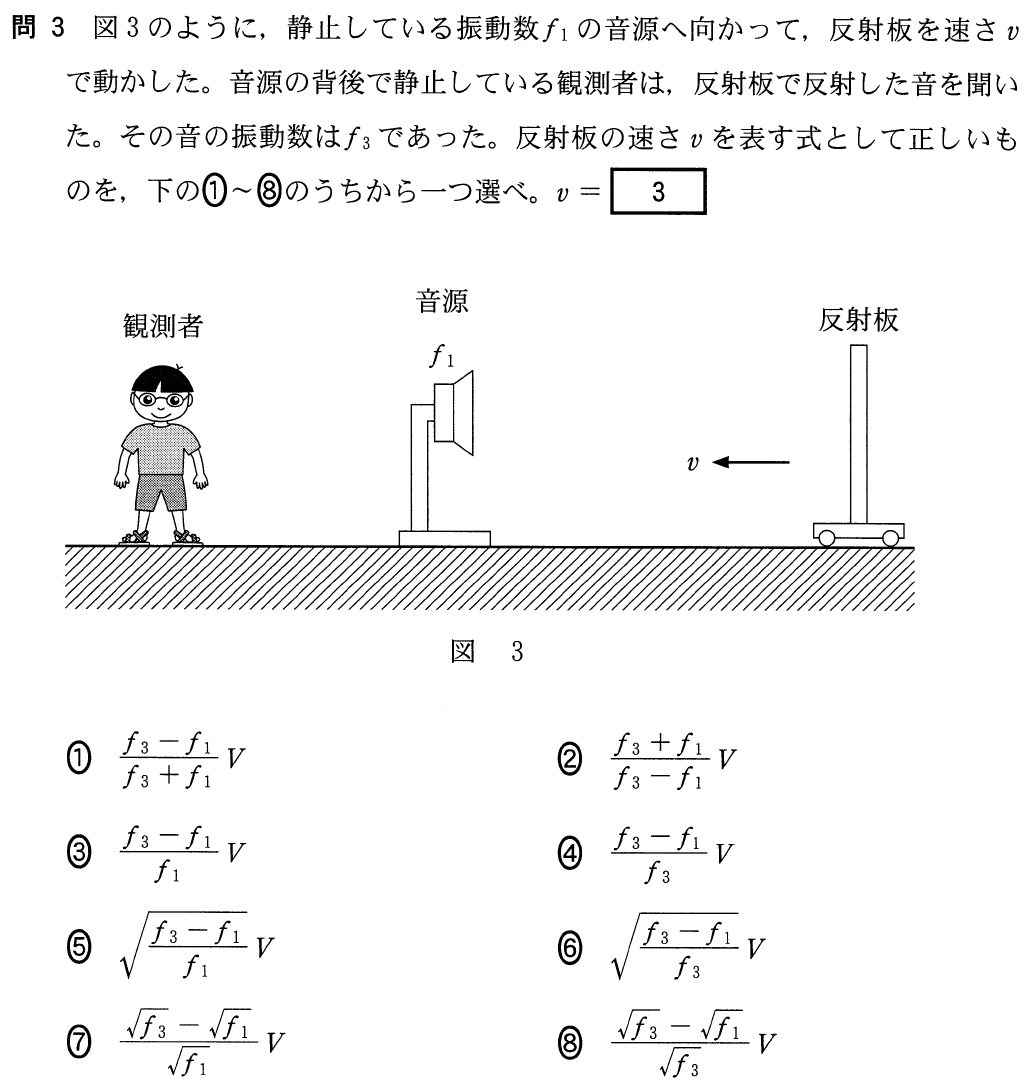
■ドップラー効果の公式は正の向きに気をつける
問1,問2の流れもあるけど,ここはドップラー効果の公式を使って,オーソドックスに解いてみよう。
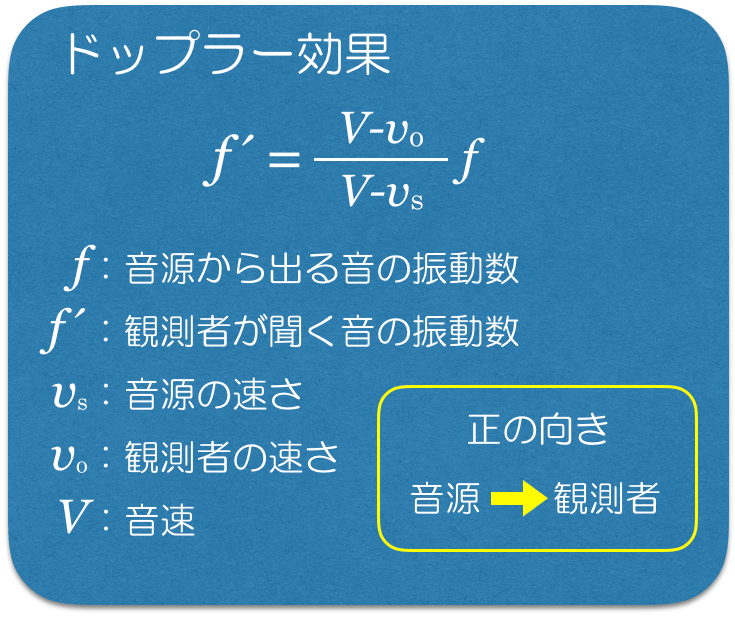
ドップラー効果の公式自体も大切だけど,正の向きが決まっていることも重要だね。特にこの反射板が動く時には正の向きが途中で変わるので,注意が必要だ。

それでは,まず反射板が受ける音の振動数を求めるのね。
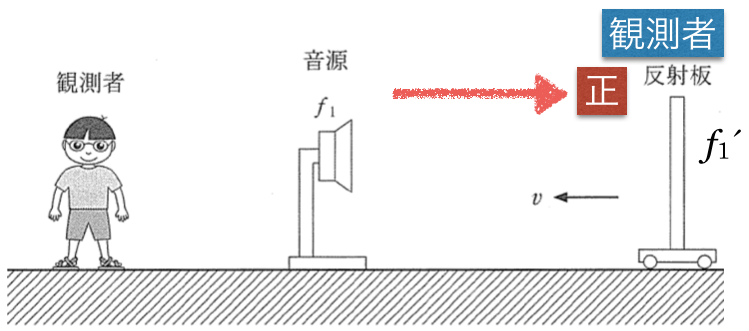
図を描いて,正の向きをちゃんと確認しておくことが大切だね。そうすると,観測者である反射板が動く向きは負ということがわかるね。
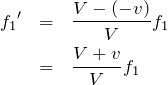
次は,反射板が
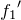
の音を出しながら,音源が動くと考えるのね。
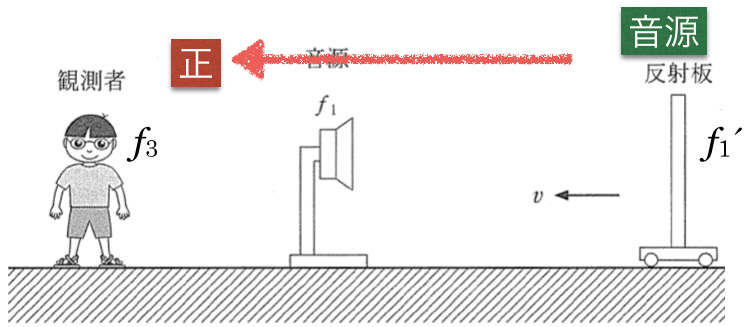
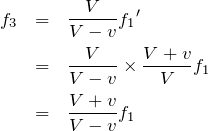
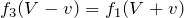
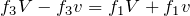
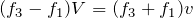
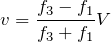





![]() より,
より,![]()
![]()

![]() なので,音が届く距離は,速さ
なので,音が届く距離は,速さ![]() 時間=
時間=![]() まで届くわ。
まで届くわ。
![]() なので,同様に
なので,同様に![]() のところにいるわ。
のところにいるわ。
![]() ということは,1秒間に
ということは,1秒間に![]() 個の波を出しているっていうこと?
個の波を出しているっていうこと?
![]() の長さの中に,
の長さの中に,![]() 個の波が入っているということになるよね。
個の波が入っているということになるよね。
![]() は,
は,![]()





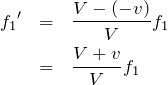
![]() の音を出しながら,音源が動くと考えるのね。
の音を出しながら,音源が動くと考えるのね。
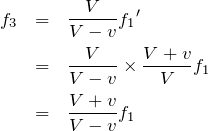
![]()
![]()
![]()
![]()
 センター試験の問題で「物理」を学ぼう!
センター試験の問題で「物理」を学ぼう!




![]() より,
より,![]()
![]()

![]() なので,音が届く距離は,速さ
なので,音が届く距離は,速さ![]() 時間=
時間=![]() まで届くわ。
まで届くわ。
![]() なので,同様に
なので,同様に![]() のところにいるわ。
のところにいるわ。
![]() ということは,1秒間に
ということは,1秒間に![]() 個の波を出しているっていうこと?
個の波を出しているっていうこと?
![]() の長さの中に,
の長さの中に,![]() 個の波が入っているということになるよね。
個の波が入っているということになるよね。
![]() は,
は,![]()





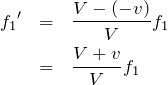
![]() の音を出しながら,音源が動くと考えるのね。
の音を出しながら,音源が動くと考えるのね。
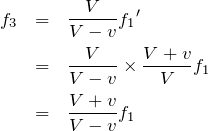
![]()
![]()
![]()
![]()