■弾性エネルギーとフックの法則
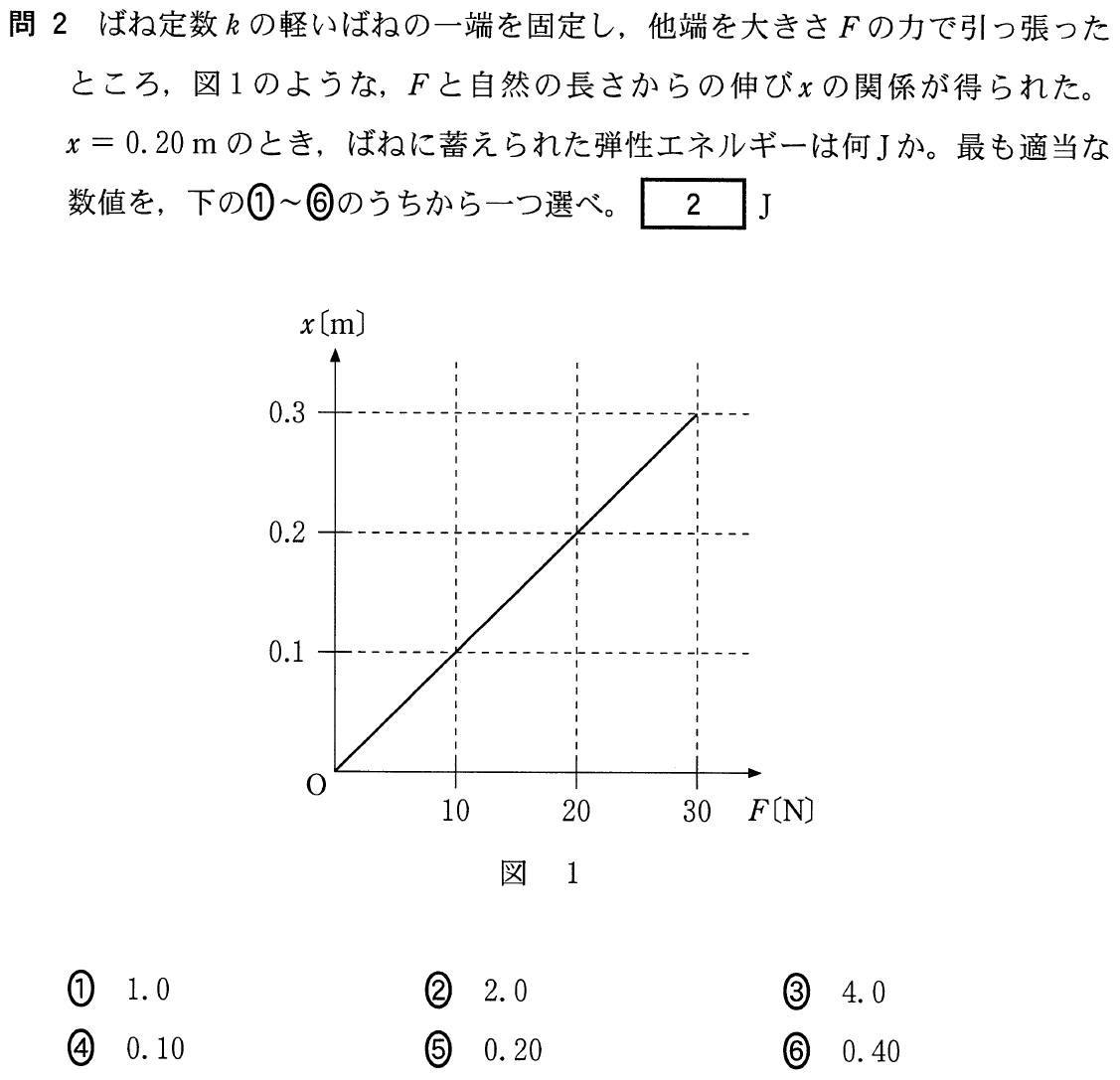
グラフから弾性エネルギーを読み取る問題ね。やったことがあるような気もするし,ないような気もするし…
グラフから弾性エネルギーを直接読み取ることはできるんだけど,まずは基本の確認をしておこうか。弾性エネルギーの式は知ってる?弾性力による位置エネルギーとも言うけど。

そうだね。問題文に「
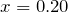
mのとき,」とあるので,あとは
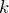
を求めればいいよね。
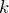
ってばね定数よね。ばね定数もグラフから分かるんだっけ?
そうだね。
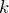
もグラフから分かるんだけど,これも基本に戻って,フックの法則から求めてみようよ。

なるほど。今は
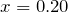
mだから,グラフから
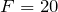
Nね。これをフックの法則の式に入れると,
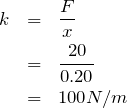
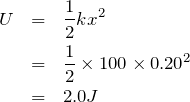
■弾性エネルギー,バネ定数をグラフから求める
弾性エネルギーやばね定数を,グラフから求めるにはどうすればいいの?
普通,フックの法則のところで出てくるグラフは,横軸がばねの伸び

で,縦軸がばねに加わる力
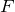
なんだよ。そのグラフ
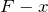
グラフだと,グラフの傾きがばね定数
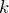
,グラフと横軸(

軸)が囲む面積が弾性エネルギーになるんだ。
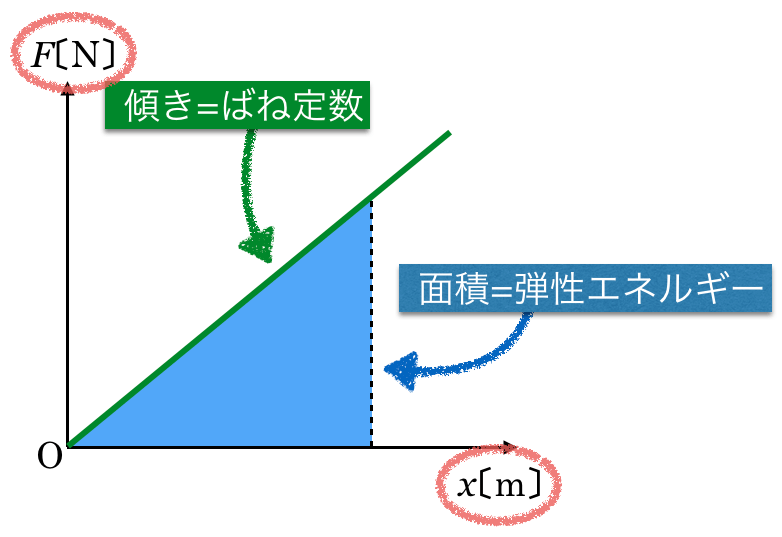
この問題は縦軸と横軸が普通とは反対ということね。反対にして考えればいいの?
そうだね。直接求めたい場合は,縦軸と横軸を入れ替えたグラフを描いてみるといいね。
どっちでもいいとは思うけど,大切なのは,「グラフの傾きはばね定数」のように,機械的に覚えちゃうと,ちょっと視点を変えた問題を出されると,対応できないので,根本からきちんと理解しておくことが大切だね。


![]() mのとき,」とあるので,あとは
mのとき,」とあるので,あとは![]() を求めればいいよね。
を求めればいいよね。![]() ってばね定数よね。ばね定数もグラフから分かるんだっけ?
ってばね定数よね。ばね定数もグラフから分かるんだっけ?![]() もグラフから分かるんだけど,これも基本に戻って,フックの法則から求めてみようよ。
もグラフから分かるんだけど,これも基本に戻って,フックの法則から求めてみようよ。
![]() mだから,グラフから
mだから,グラフから![]() Nね。これをフックの法則の式に入れると,
Nね。これをフックの法則の式に入れると,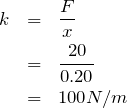
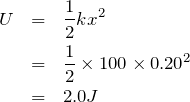
![]() で,縦軸がばねに加わる力
で,縦軸がばねに加わる力![]() なんだよ。そのグラフ
なんだよ。そのグラフ![]() グラフだと,グラフの傾きがばね定数
グラフだと,グラフの傾きがばね定数![]() ,グラフと横軸(
,グラフと横軸(![]() 軸)が囲む面積が弾性エネルギーになるんだ。
軸)が囲む面積が弾性エネルギーになるんだ。