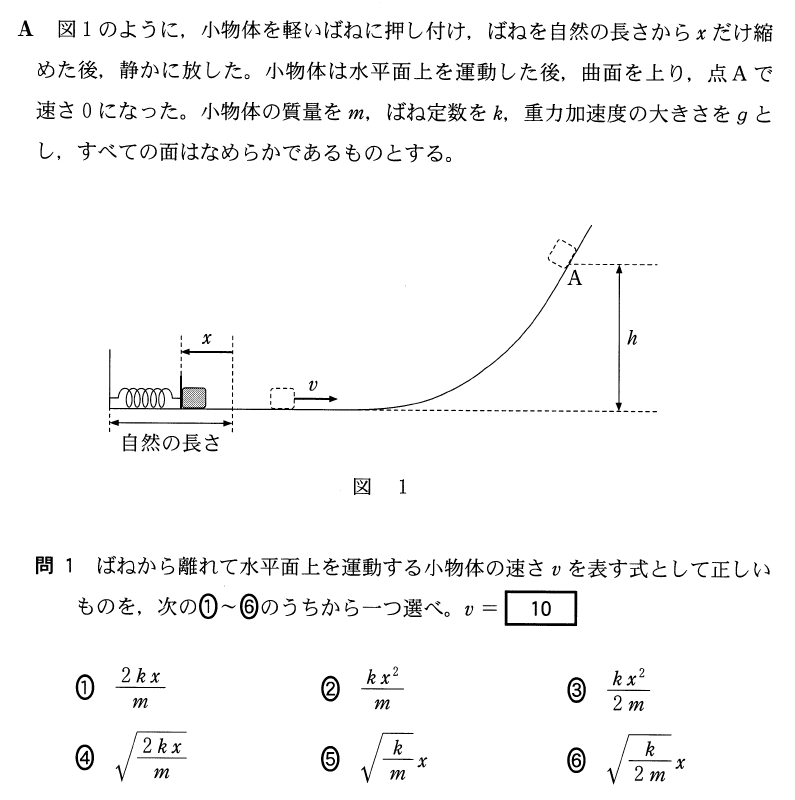
そうだね。力学的エネルギー保存の法則を使うときのポイントは、どの点で式を立てるのかをきちんと押さえておくことだよ。
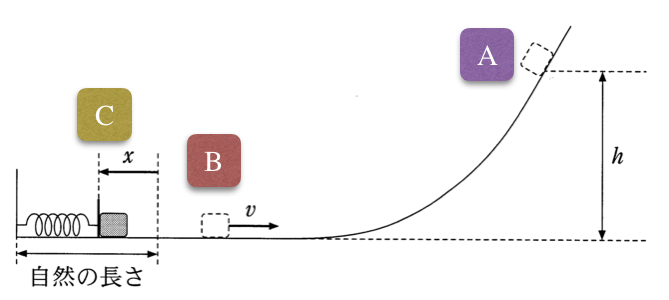
問題文には、曲面上の最高点の位置が「A」という名前になっているので、他の点は図のように「B」、「C」としておこう。
そもそも「力学的エネルギー」って何だか分かってる?
確か、「運動エネルギーと位置エネルギーの和」よね。
そう。まず大切なのは「和」ということだね。足し算をするんだね。もう一つ大切なのは、位置エネルギーにはいくつかあって、この分野では一般的に、「重力による位置エネルギー」と「弾性力による一エネルギー」があるよね。他にも、「万有引力による位置エネルギー」や「静電気力による位置エネルギー」なんかもあるので、必要なときには思い出してね。
この問題で出てくる力学的エネルギーをまとめるとこうだよ。

ここまでは大丈夫。最初に求めるのは

だから、「C」と「B」で力学的エネルギー保存の法則の式を立てればいいのよね。
そうだね。「B」と「C」で考えると、重力による位置エネルギーは同じなので、式の上では書かなくてもいいよね。
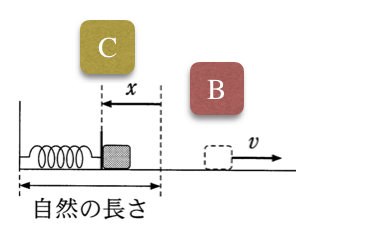

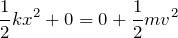
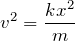
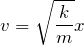
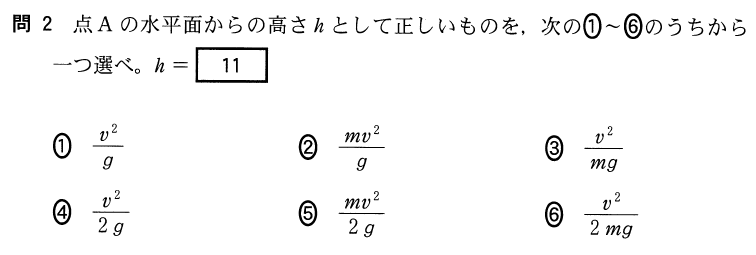
そうだね。問1でもやったけど、2点を決めて力学的エネルギー保存の法則を使って式を立てるよね。問2では、どの2点で式を立てよう?

「B」と「A」でいいわよね。「C」と「A」でもいいのかな?
そう。どっちでもいいんだ。だけど問題の選択肢を見ると、
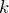
や

は無いけど、

はあるので、「C」を使わない方がいいね。
実際は「C」を使っても、問1で立てた関係式を使って正解は導き出せるけど、少し遠回りだからね。
それじゃあ、「B」と「C」で力学的エネルギー保存の法則を立ててみるわ。
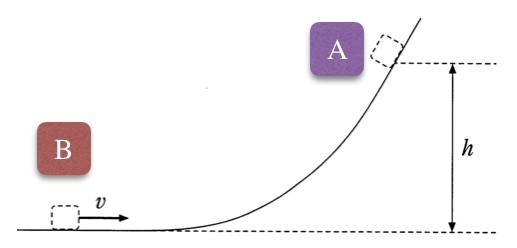
今度は弾性力による位置エネルギーは関係ないので、式の上では必要ないね。

重力による位置エネルギーの基準を水平面として、式を立てると、
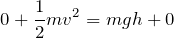
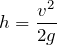



![]() だから、「C」と「B」で力学的エネルギー保存の法則の式を立てればいいのよね。
だから、「C」と「B」で力学的エネルギー保存の法則の式を立てればいいのよね。

![]()
![]()
![]()


![]() や
や![]() は無いけど、
は無いけど、![]() はあるので、「C」を使わない方がいいね。
はあるので、「C」を使わない方がいいね。

![]()
![]()
 センター試験の問題で「物理」を学ぼう!
センター試験の問題で「物理」を学ぼう!


![]() だから、「C」と「B」で力学的エネルギー保存の法則の式を立てればいいのよね。
だから、「C」と「B」で力学的エネルギー保存の法則の式を立てればいいのよね。

![]()
![]()
![]()


![]() や
や![]() は無いけど、
は無いけど、![]() はあるので、「C」を使わない方がいいね。
はあるので、「C」を使わない方がいいね。

![]()
![]()