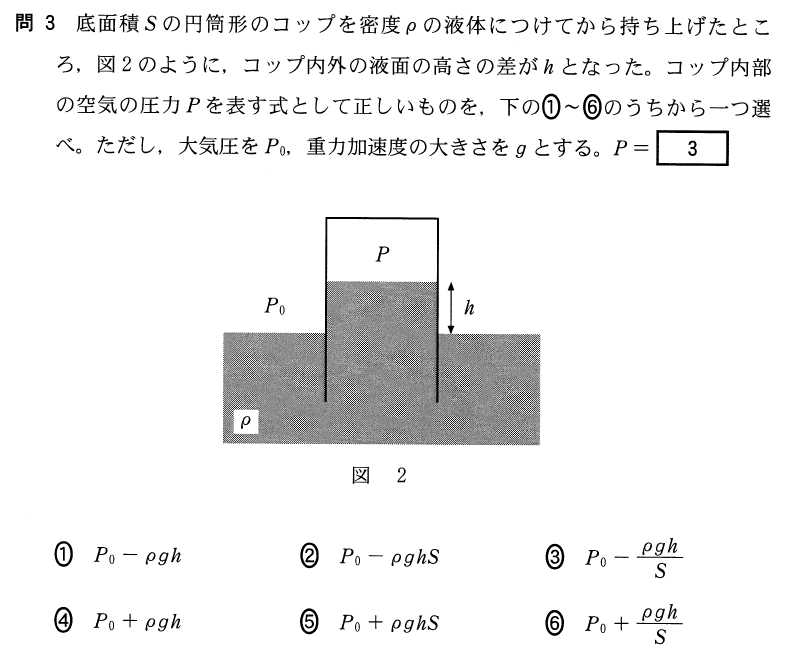
そうだね。力学の問題は、とりあえず力の矢印を描いてみる、という手があるんだけど、液体が出てくる問題は力の矢印を描きにくいんだよね。
そうなのよ。液体に力の矢印描くのも変だし、コップにはたらく力の矢印を描いても、何も出てこない。
そうなんだよね。このような問題の場合、「同じ高さでは、圧力が同じ」という関係を使うんだ。気体や液体だと成り立つんだよね。問題によっては「同じ高さ」というより、「同じ深さ」という表現の方がいいかもね。
同じ深さだと水圧は同じ、っていうのは聞いたことがある。確かこんな式だったかな。
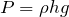
良く覚えているね。使うことが少ないから忘れがちな式だよね。この式は確かに深さ
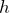
が同じであれば、水圧も同じということだね。
これは知ってるんだけど、この問題では「深さ」は関係なさそう。
そうだね。なのでやっぱり「同じ高さでは、圧力が同じ」という関係を使ってみよう。分かりやすい「同じ高さ」はここかな。
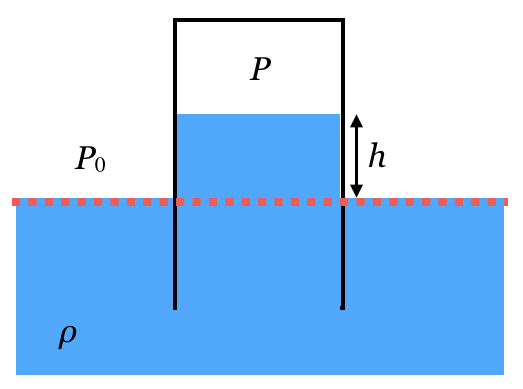
それじゃあ最初に、コップの周りの液面を押す圧力はいくらかな。
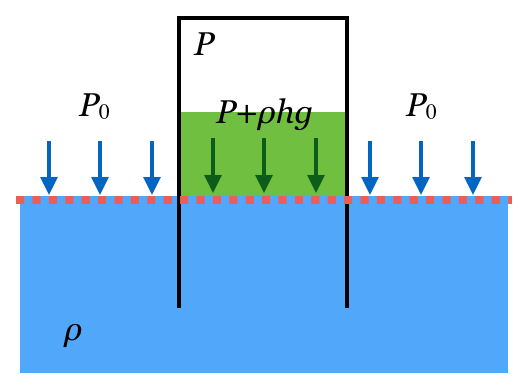
それって、大気圧のことよね。なので、
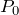
ね。
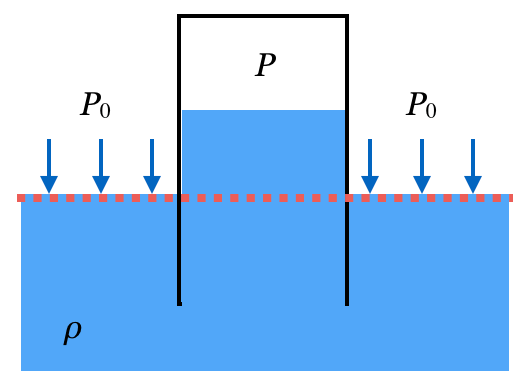
その通り。そこは大丈夫かな。この圧力と、コップの中の同じ高さの圧力が同じなんだね。コップの中の赤い線のところの圧力は分かるかな?
そうそう、その液体も考えて赤い線の高さでの圧力を考えるんだね。
この緑色の部分ね。緑色の部分の液体の体積は底面積×高さだから、
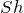
ね。
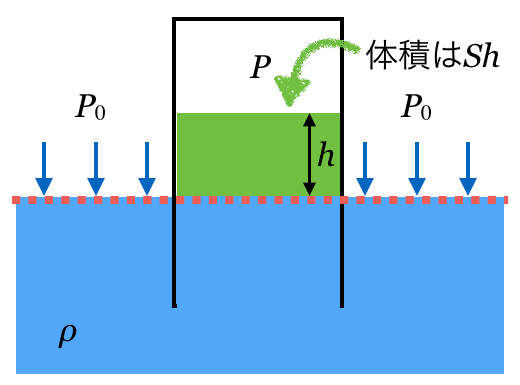
体積は分かるんだけど、質量はどうすればいいんだっけ?
密度を使うんだね。そもそも密度を質量と体積で表すとどうなる?
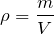
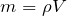
じゃあ、今求めたい「圧力」って、どうやって求めるんだっけ?
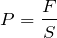
それじゃあ、コップの中の赤い線のところでの、力って何だ?
赤い線のところに加わる力って、その上にある液体の「重さ」でいいの?
そうだね。「重力」っていう力の大きさのことを「重さ」っていうんだよね。ただ、赤い線の高さには上にある液体の重さ以外にも力が加わってるんだよ。
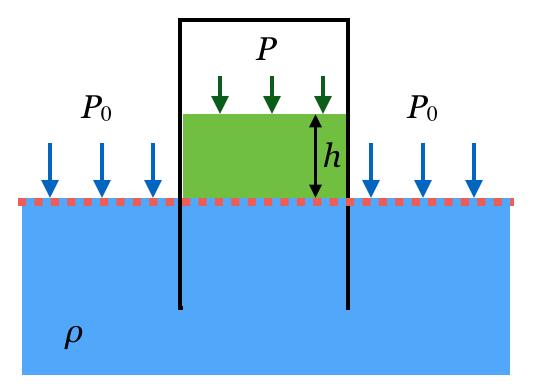
じゃあ、まず、赤い線上の部分の液体の重さは、
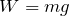
だから、
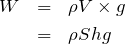
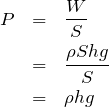
いいね。それで、コップの中の空気の圧力
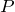
を加えて、同じ高さの大気圧
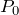
と等しいという式を立てて計算すると?
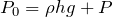
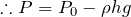

![]()
![]() が同じであれば、水圧も同じということだね。
が同じであれば、水圧も同じということだね。
![]() ね。
ね。
![]() ね。
ね。
![]()
![]()
![]()

![]() だから、
だから、![]()
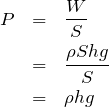
![]() を加えて、同じ高さの大気圧
を加えて、同じ高さの大気圧![]() と等しいという式を立てて計算すると?
と等しいという式を立てて計算すると?
![]()
![]()
 センター試験の問題で「物理」を学ぼう!
センター試験の問題で「物理」を学ぼう!
![]()
![]() が同じであれば、水圧も同じということだね。
が同じであれば、水圧も同じということだね。
![]() ね。
ね。
![]() ね。
ね。
![]()
![]()
![]()

![]() だから、
だから、![]()
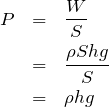
![]() を加えて、同じ高さの大気圧
を加えて、同じ高さの大気圧![]() と等しいという式を立てて計算すると?
と等しいという式を立てて計算すると?
![]()
![]()